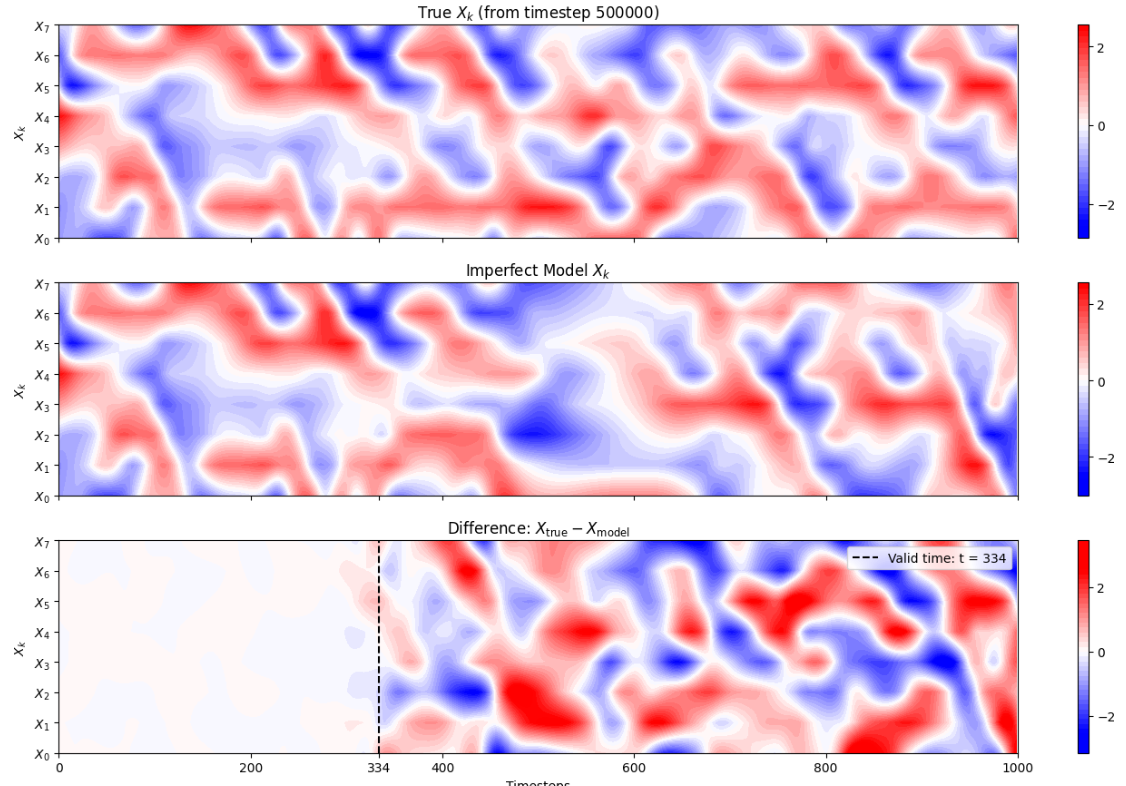
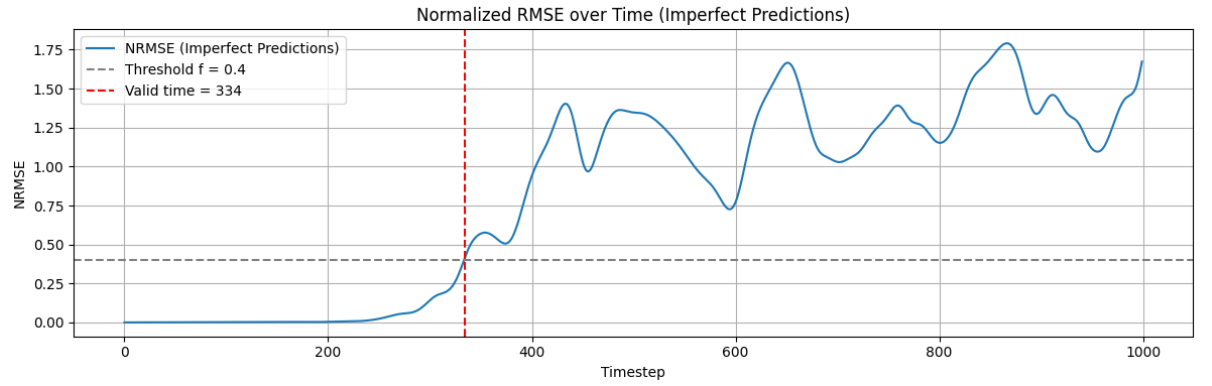
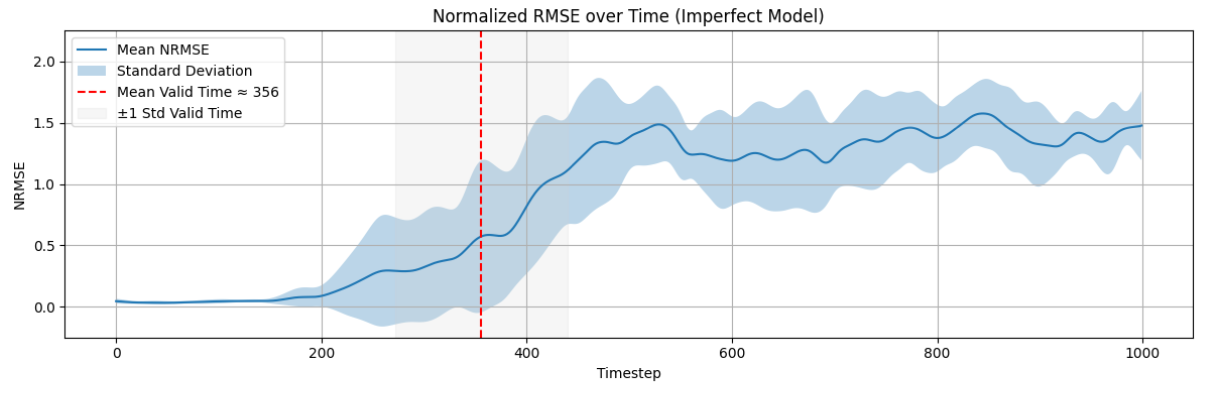
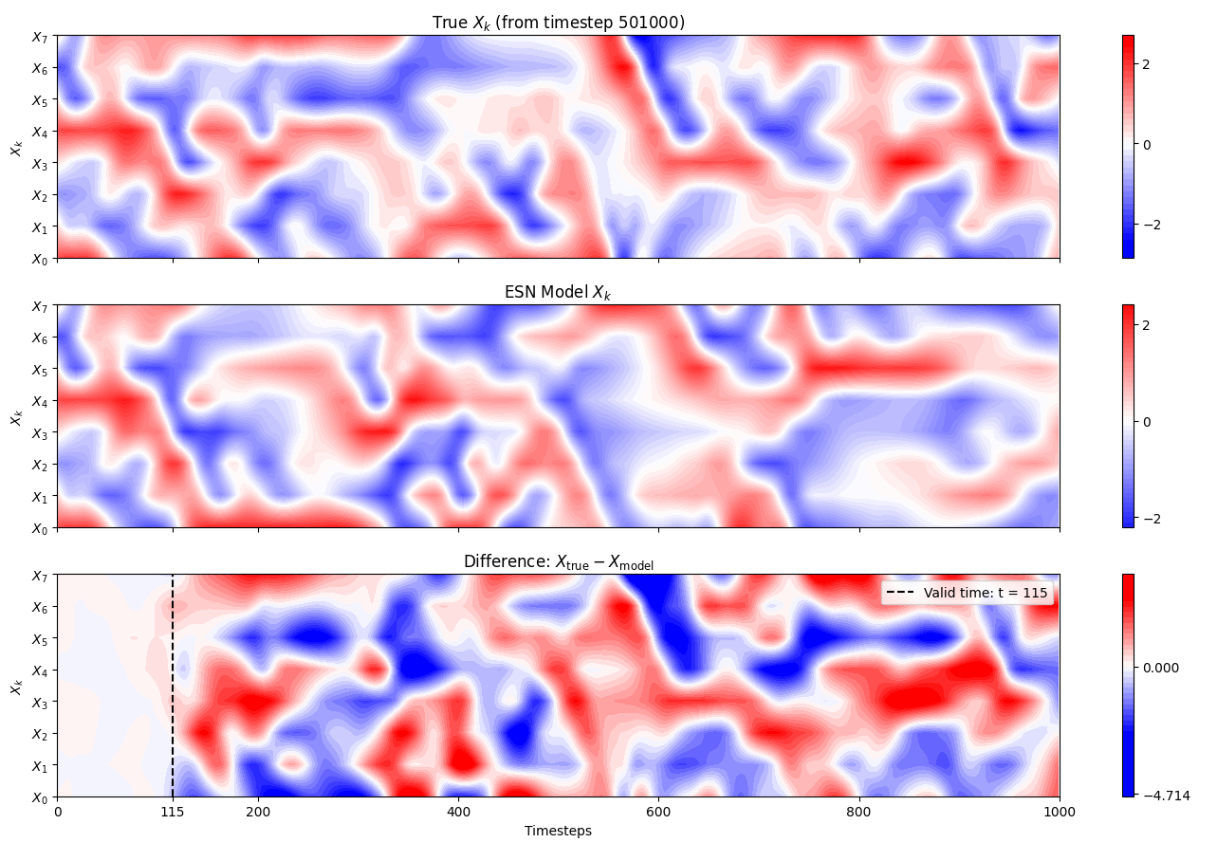
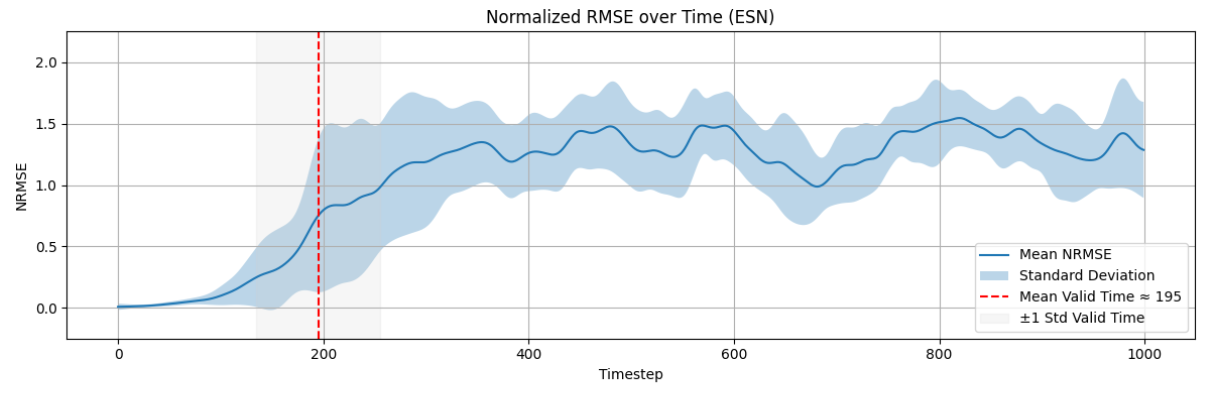
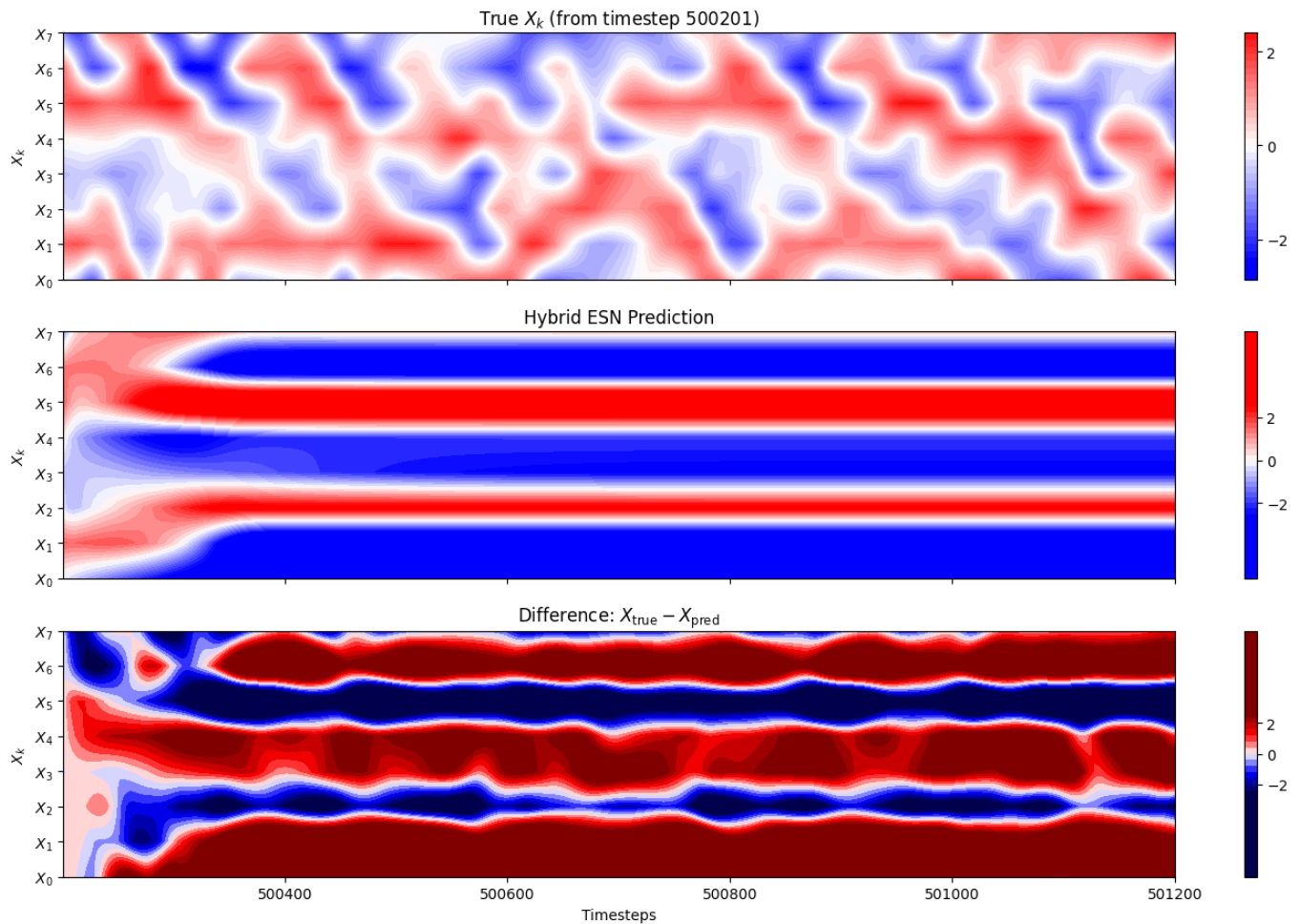
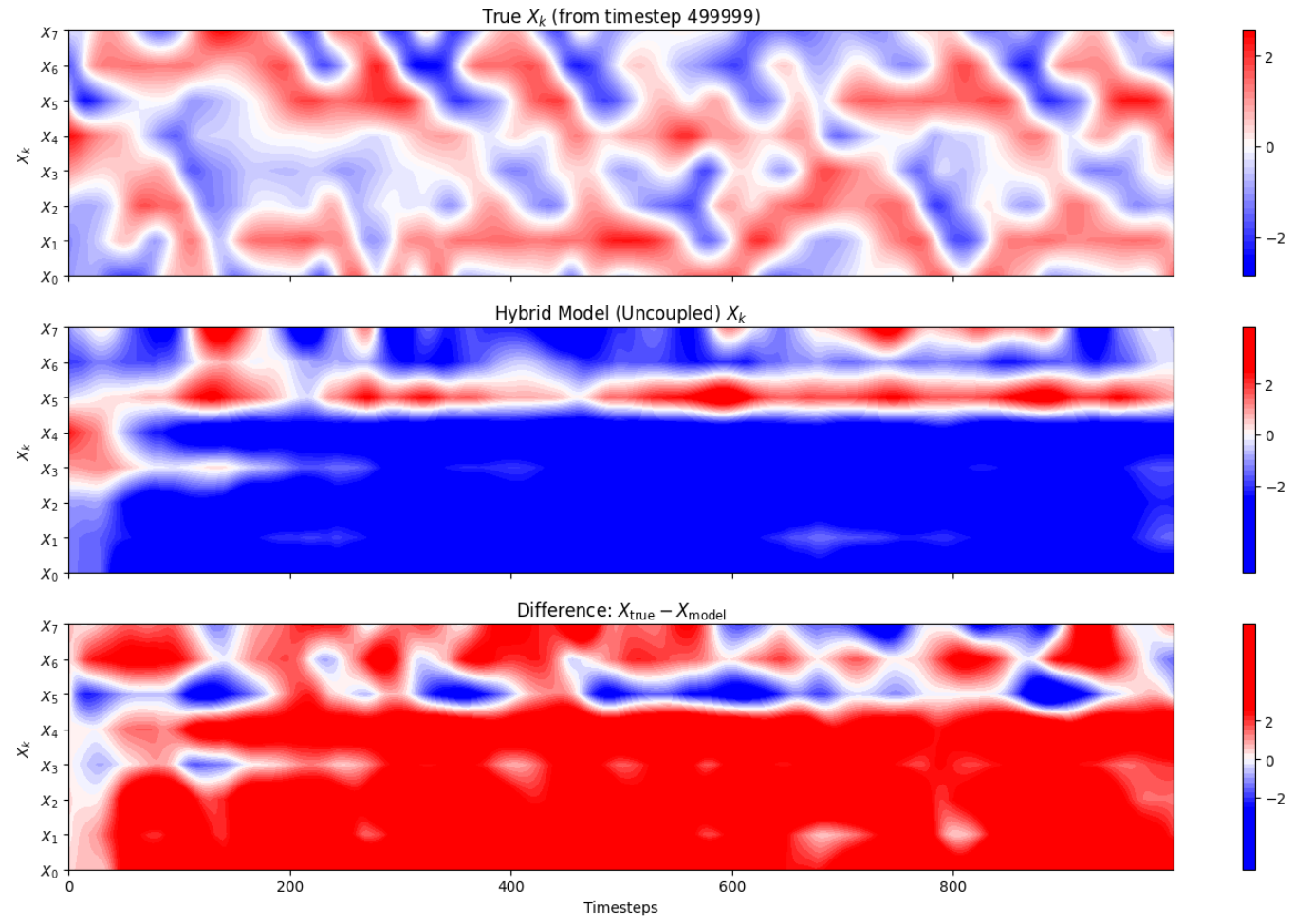
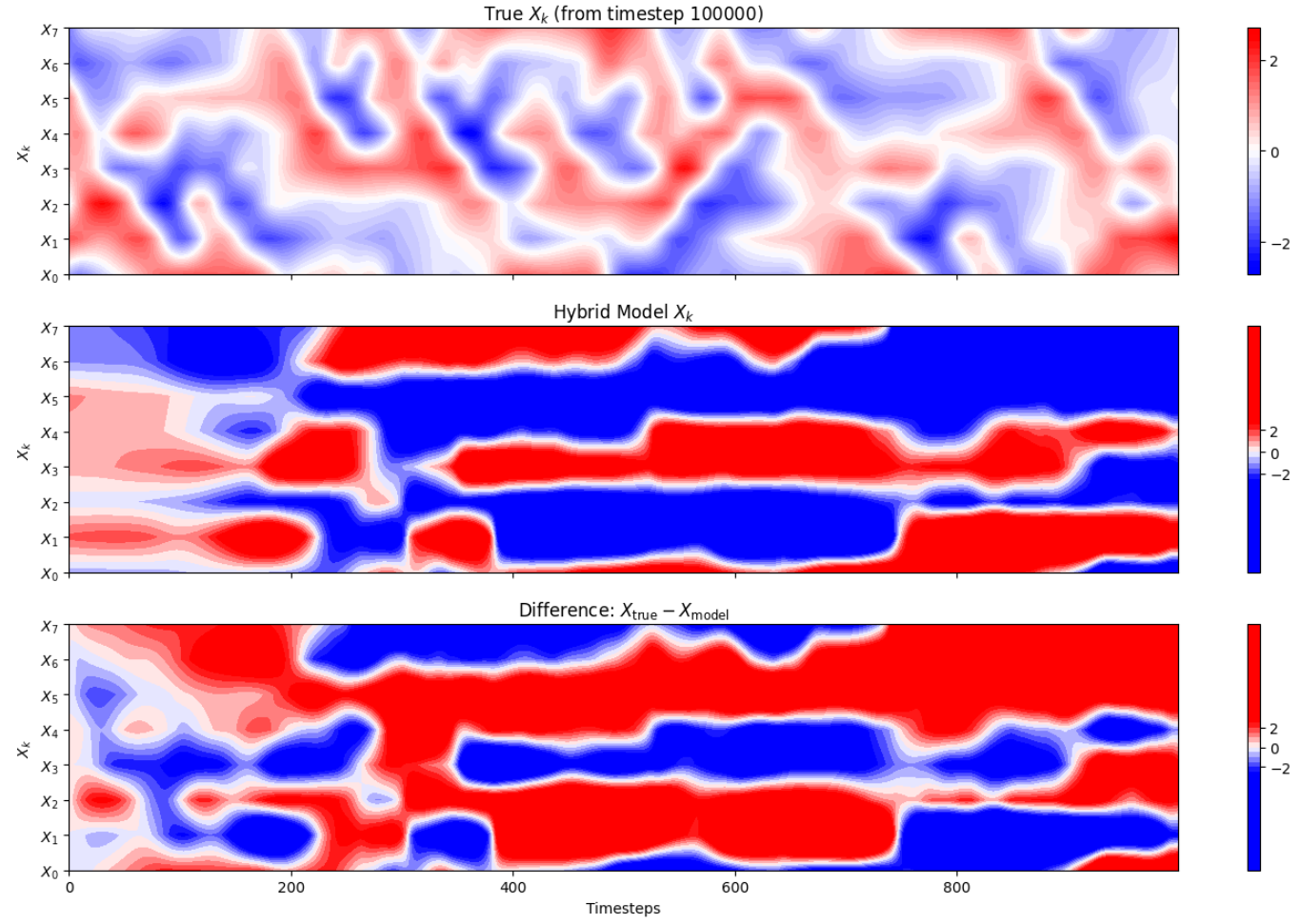
Results
Refrencese
[1] Ashesh Chattopadhyay, Pedram Hassanzadeh, and Devika Subramanian. Data-driven pre-dictions of a multiscale lorenz 96 chaotic system using machine-learning methods: reservoircomputing, artificial neural network, and long short-term memory network. Nonlinear Pro-cesses in Geophysics, 27(3):373–389, July 2020.
[2] Ashesh Chattopadhyay, Adam Subel, and Pedram Hassanzadeh. Data-driven super-parameterization using deep learning: Experimentation with multiscale lorenz 96 systemsand transfer learning. Journal of Advances in Modeling Earth Systems, 12(11), November2020.
[3] Geir Evensen. The ensemble kalman filter: Theoretical formulation and practical implemen-tation. Ocean Dynamics, 53(4):343–367, 2003.
[4] Debdipta Goswami, Artur Wolek, and Derek A. Paley. Data-driven estimation using anecho-state neural network equipped with an ensemble kalman filter. In 2021 AmericanControl Conference (ACC), pages 2549–2554, 2021.
[5] NASA/GSFC. Application of the ensemble kalman filter (enkf) to lorenz’s 1963 model,2010. Exploring Our Magnetic Earth.
[6] Jaideep Pathak, Alexander Wikner, Rebeckah Fussell, Sarthak Chandra, Brian R. Hunt,Michelle Girvan, and Edward Ott. Hybrid forecasting of chaotic processes: Using machinelearning in conjunction with a knowledge-based model. Chaos: An Interdisciplinary Journalof Nonlinear Science, 28(4), April 2018.

